Event Triggered Control and Stability

Introduction

the idea of event triggered system is that we instead of online feedback , define a policy and update the feedback signal based on that policy, the gain we get is mostly computational although it can also gives us other gains too.

preliminaries

consider a state space system like:

\[\dot{x} = Ax + Bu \underset{u = kx(t)}{\implies} \dot{x} = (A+Bk)x \quad \text{input feedback}\] \[V(x) = {x(t)}^TPx(t) > 0 \implies P > 0 \quad \text{Lyapunov stability}\] \[\dot{V}(x) = \dot{x}^T(t)Px(t) + x^T(t)P\dot{x}(t) < 0\] \[\underset{\text{state space}}{\implies} {x(t)}^T (A+Bk)^T P x(t) + x^T(t)P(A+Bk)x(t) < 0\] \[\implies x^T(t)\underbrace{[\left (A+Bk)^TP + P(A+Bk) \right]}_{N.D.} x(t) < 0\]

we call this Negative Definite matrix Q.

\[\text{stability condition} : \begin{cases} P > 0 \\ (A+Bk)^TP+ P(A+Bk) < 0\\ \end{cases}\]

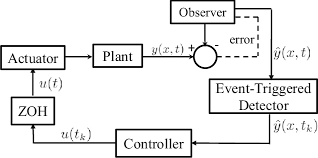
Event-Based

\[u = kx(\tau) \implies \dot{x}(t) = Ax(t) + Bkx(\tau)\] \[\dot{V}(x) = \dot{x}(t)^TPx(t) + x(t)^TP\dot{x}(t) < 0\] \[\dot{V}(x) = \underbrace{x^T(\tau) (Bk)^TPx(t)} + x^T(t)PBkx(\tau) + \underbrace{x^T(t)A^TPx(t)} + x^T(t)PAx(t) < 0\]

by defining error singal, we have:

\[e(t) = x(t) - x(\tau) \implies x(\tau) = x(t) - e(t)\]

and by subtituding that in equation the first term like not event-driven method gonna emerge just instead of each \(x(\tau)\) we put the \(x(t)\) and merge it to make the first term then by subtituding the \(-e(t)\) we have to subtracting terms:

\[\implies x^T(t)[\left (A+Bk)^TP + P(A+Bk) \right] x(t) - e(t)^T(Bk)^TPx(t) - x^T(t)PBke(t) < 0\]

and since both \(e(t)^T(Bk)^TPx(t)\) and \(x^T(t)PBke(t)\) are numbers we can merge them into: \(\implies x^T(t)[\left (A+Bk)^TP + P(A+Bk) \right] x(t) - 2e(t)^T(Bk)^TPx(t) < 0\)

\[\underset{\text{previous part }}{\implies} x^T(t)Q x(t) - 2e(t)^T(Bk)^TPx(t) < 0\]

this yeilds

\[- 2e(t)^T(Bk)^TPx(t) < - x^T(t)Q x(t)\]

from this we derive: \(|e(t)||Bk||x(t)| < - \lambda_{min}(Q)||x||^2 \leq - x^T(t)Q x(t)\)

this yields the event triggered condition we were looking for:

\[|e(t)| \leq - \frac{\lambda_{min}(Q) ||x(t)||}{2 ||Bk||} \quad \text{event-triggered condtion}\]

why is this the event-triggered condtion?

basically the idea here is to find some kind of condition with two intentions:

1. we should keep the \(\dot{V}\) negetive to guarantee stability
2. find some condition on e(t)

why we care about e(t)?

because if you recall \(e(t) = x(t) - x(\tau)\) , and we by closing the relay and update the feedback signal we can make it zero, so the procedure is like this in event triggered:

1. find an upper bound on e(t) which gaurantee stability which gonna lead to this: f(e(t)) < ...
2. if we see the bound has been violated we update the singal which means we put forfully put e(t) to zero.